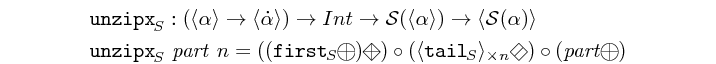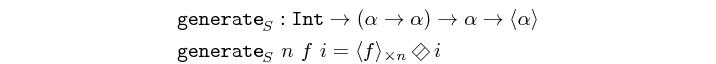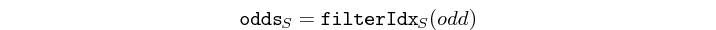| Copyright | (c) George Ungureanu KTH/ICT/ESY 2016 |
|---|---|
| License | BSD-style (see the file LICENSE) |
| Maintainer | ugeorge@kth.se |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | Safe |
| Language | Haskell2010 |
ForSyDe.Atom.Skel.Vector
Description
This module defines the data type Vector as a categorical type, and implements
the atoms for the Skeleton class. Algorithmic skeletons for Vector are mostly
described in their factorized form (see the
factorization theorem). For practical
reasons some skeletons are implemented as recurrences , but their factorized form
is still documented.
Useful links:
- ForSyDe.Atom contains general guidelines for using the API
- ForSyDe.Atom.Skel documents details about the internals of the Skeleton layer, the atoms and some basic generic patterns.
- ForSyDe.Atom.Skel.Vector.Matrix contains a collection of patterns for
working with 2-dimensional
Vectors. - ForSyDe.Atom.Skel.Vector.Cube contains a collection of patterns for working
with 3-dimensional
Vectors. - ForSyDe.Atom.Skel.Vector.DSP contains a collection of patterns commonly used in signal processing designs.
- the naming convention rules on how to interpret the function names based on their number of inputs and outputs.
Synopsis
- data Vector a
- null :: Vector a
- unit :: a -> Vector a
- (<++>) :: Vector a -> Vector a -> Vector a
- vector :: [a] -> Vector a
- fromVector :: Vector a -> [a]
- indexes :: Vector Int
- isNull :: Vector a -> Bool
- (<:) :: Vector a -> a -> Vector a
- farm22 :: (a1 -> a2 -> (b1, b2)) -> Vector a1 -> Vector a2 -> (Vector b1, Vector b2)
- reduce :: (a -> a -> a) -> Vector a -> a
- prefix :: (b -> b -> b) -> Vector b -> Vector b
- suffix :: (b -> b -> b) -> Vector b -> Vector b
- pipe :: Vector (a -> a) -> a -> a
- (=/=) :: Vector (a -> a) -> a -> Vector a
- recur :: Vector (a -> a) -> a -> Vector a
- cascade2 :: (a2 -> a1 -> a -> a -> a) -> Vector (Vector a2) -> Vector (Vector a1) -> Vector a -> Vector a -> Vector a
- mesh2 :: (a2 -> a1 -> a -> a -> a) -> Vector (Vector a2) -> Vector (Vector a1) -> Vector a -> Vector a -> Vector (Vector a)
- length :: Num p => Vector a -> p
- index :: Vector a2 -> Vector Int
- fanout :: t -> Vector t
- fanoutn :: (Ord t, Num t) => t -> a -> Vector a
- generate :: (Ord t, Num t) => t -> (a -> a) -> a -> Vector a
- iterate :: (Ord t, Num t) => t -> (a -> a) -> a -> Vector a
- first :: Vector a -> a
- last :: Vector a -> a
- inits :: Vector a -> Vector (Vector a)
- tails :: Vector a -> Vector (Vector a)
- init :: Vector a -> Vector a
- tail :: Vector a -> Vector a
- concat :: Vector (Vector a) -> Vector a
- reverse :: Vector a -> Vector a
- group :: Int -> Vector a -> Vector (Vector a)
- shiftr :: Vector a -> a -> Vector a
- shiftl :: Vector a -> a -> Vector a
- rotr :: Vector a -> Vector a
- rotl :: Vector a -> Vector a
- rotate :: Int -> Vector a -> Vector a
- take :: Int -> Vector a -> Vector a
- drop :: Int -> Vector a -> Vector a
- takeWhile :: (a -> Bool) -> Vector a -> Vector a
- filterIdx :: (Int -> Bool) -> Vector a -> Vector a
- odds :: Vector a -> Vector a
- evens :: Vector a -> Vector a
- stride :: Int -> Int -> Vector a -> Vector a
- get :: Int -> Vector a -> Maybe a
- (<@) :: Vector a -> Int -> Maybe a
- (<@!) :: Vector p -> Int -> p
- gather1 :: Vector Int -> Vector a -> Vector (Maybe a)
- (<@>) :: Vector a -> Vector Int -> Vector (Maybe a)
- replace :: Int -> a -> Vector a -> Vector a
- scatter :: Vector Int -> Vector a -> Vector a -> Vector a
- zipx :: MoC e => Vector ((Vector a -> Vector a -> Vector a) -> Fun e (Vector a) (Fun e (Vector a) (Ret e (Vector a)))) -> Vector (Stream (e a)) -> Stream (e (Vector a))
- unzipx :: MoC e => (Vector a -> Vector (Ret e a)) -> Integer -> Stream (e (Vector a)) -> Vector (Stream (e a))
Vector data type
Although the name Vector is borrowed from <ForSyDe-Atom.html#reekie95
[Reekie95]> since it is more suggestive in the context of process networks, the
Vector type is in fact modeling an infinite list defined as a category in
[Skillicorn05]. According to this definition it
should be implemented as following:
data Vector a = Null -- null element
| Unit a -- singleton vector
| Vector a <++> Vector a -- concatenate two vectorsThis construction suggests the possibility of splitting a Vector into multiple
parts and evaluating it in parallel. For simplicity and to ensure that the
structure is flat and homogeneous, Vector is implemented using the same
constructors as a regular Haskell list (see below). When defining skeletons of
vectors we will not use the real constructors though, but the theoretical ones
defined above and provided as functions. This way we align ForSyDe-Atom's
Vector type with the skeleton theory and its theorems.
Another particularity of Vector is that it instantiates the reduction atom =\=
as a right fold, as it is the most efficient lazy implementation of lists. As a
consequence reduction is performed from right to left. This is noticed
especially in the case of pipeline-based skeletons (see definition of
pipe as a reduction with the right-associative composition
operator .) is performed from right to left. Thus for reduce-based skeletons
(e.g. prefix, suffix, recur, cascade, mesh) the result vectors shall be
read from end to beginning.
Constructors
| Null | Null element. Terminates a vector. |
| a :> (Vector a) infixr 3 | appends an element at the head of a vector. |
Instances
| Functor Vector Source # | Provides an implementation for |
| Applicative Vector Source # | Provides an implementation for |
| Foldable Vector Source # | Provides an implementation for |
Defined in ForSyDe.Atom.Skel.Vector.Core Methods fold :: Monoid m => Vector m -> m # foldMap :: Monoid m => (a -> m) -> Vector a -> m # foldMap' :: Monoid m => (a -> m) -> Vector a -> m # foldr :: (a -> b -> b) -> b -> Vector a -> b # foldr' :: (a -> b -> b) -> b -> Vector a -> b # foldl :: (b -> a -> b) -> b -> Vector a -> b # foldl' :: (b -> a -> b) -> b -> Vector a -> b # foldr1 :: (a -> a -> a) -> Vector a -> a # foldl1 :: (a -> a -> a) -> Vector a -> a # elem :: Eq a => a -> Vector a -> Bool # maximum :: Ord a => Vector a -> a # minimum :: Ord a => Vector a -> a # | |
| Skeleton Vector Source # | Ensures that |
Defined in ForSyDe.Atom.Skel.Vector.Core | |
| Eq a => Eq (Vector a) Source # | |
| Read a => Read (Vector a) Source # | The vector 1 :> 2 :> Null is read using the string "<1,2>". |
| Show a => Show (Vector a) Source # | The vector 1 :> 2 :> Null is represented as <1,2>. |
| Plottable a => Plottable (Vector a) Source # | Vectors of plottable types |
| Plottable a => Plot (Vector a) Source # | For plotting vectors of coordinates |
"Constructors"
Theoretical constructors for the Vector type, used in the definition of
skeletons as catamorphisms.
(<++>) :: Vector a -> Vector a -> Vector a infixr 5 Source #
Constructs a vector by appending two existing vectors.
>>>unit 1 <++> unit 2<1,2>
Utilities
fromVector :: Vector a -> [a] Source #
Converts a vector to a list.
indexes :: Vector Int Source #
Creates the infinite vector:
<1,2,3,4,...>
Used mainly for operation on indexes.
Skeletons
Algorithmic skeletons on vectors are mainly presented in terms of compositions
of the atoms associated with the Skeleton Layer. When defining them, we use the
following operators:
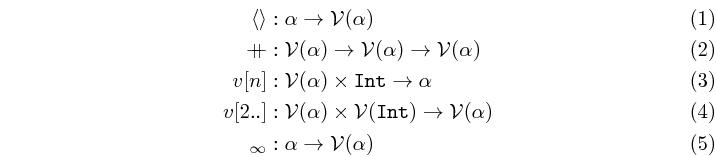
where:
- (1) is the
unitconstructor, constructing a singleton vector. - (2) is the
<++>constructor, concatenating two vectors. - (3) is the
<@!selector. The subscript notation is used to denote element at position n in a vector. - (4) suggests an arbitrary selector which returns a vector with another one's
elements, based on some indices. The shown example is an alternative notation for
the
tailskeleton.
Functional networks
This sub-category denotes skeletons (patterns) which are take functions as
arguments. If the functions are MoC layer entities,
i.e. processes, then these patterns are capable of constructing parallel process
networks. Using the applicative mechanism, the designer has a high degree of
freedom when customizing process networks through systematic partial application,
rendering numerous possible usages for the same pattern. To avoid
over-encumbering the figures, they depict small test cases, which might not
expose the full potential of the constructors.
see the naming convention rules on how to interpret, use and develop your own constructors.
Arguments
| :: (a1 -> a2 -> (b1, b2)) | function (e.g. process) |
| -> Vector a1 | first input vector |
| -> Vector a2 | second input vector |
| -> (Vector b1, Vector b2) | two output vectors |
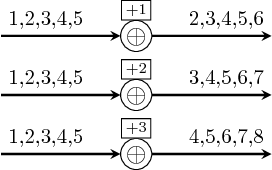
farm is simply the Vector instance of the skeletom farm
pattern (see farm22). If the function taken
as argument is a process, then it creates a farm network of data
parallel processes.
Constructors: farm[1-4][1-4].
>>>let v1 = vector [1,2,3,4,5]>>>S.farm21 (+) v1 v1<2,4,6,8,10>>>>let s1 = SY.signal [1,2,3,4,5]>>>let v2 = vector [s1,s1,s1]>>>S.farm11 (comb11 (+1)) v2<{2,3,4,5,6},{2,3,4,5,6},{2,3,4,5,6}>>>>S.farm21 (\x -> comb11 (+x)) v1 v2<{2,3,4,5,6},{3,4,5,6,7},{4,5,6,7,8}>
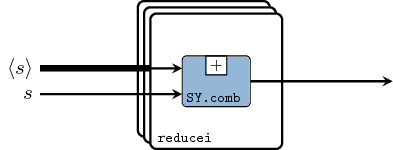
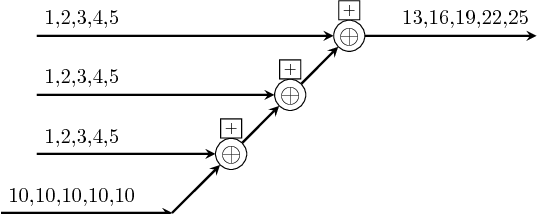
reduce :: (a -> a -> a) -> Vector a -> a Source #
As the name suggests, it reduces a vector to an element based on an associative function. If the function is not associative, it can be treated like a pipeline.
Vector instantiates the skeletons for both
reduce and reducei.
>>>let v1 = vector [1,2,3,4,5]>>>S.reduce (+) v115>>>let s1 = SY.signal [1,2,3,4,5]>>>let s2 = SY.signal [10,10,10,10,10]>>>let v2 = vector [s1,s1,s1]>>>S.reduce (comb21 (+)) v2{3,6,9,12,15}>>>S.reducei (comb21 (+)) s2 v2{13,16,19,22,25}
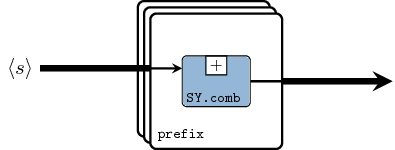
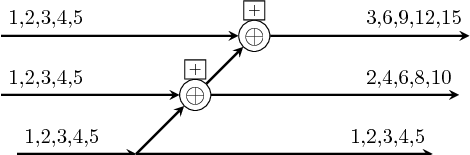
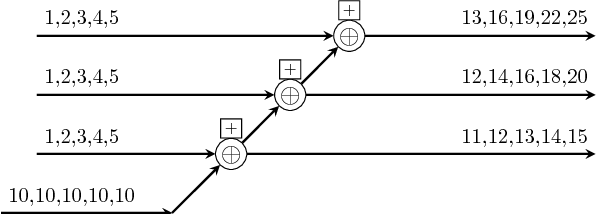
prefix :: (b -> b -> b) -> Vector b -> Vector b Source #
prefix peforms the parallel prefix operation on a vector.
Equivalent process networks are constructed if processes are passed
as arguments.
Similar to reduce and reducei, two versions prefix and
prefixi are provided.
>>>let v1 = vector [1,2,3,4,5]>>>prefix (+) v1<15,14,12,9,5>>>>let s1 = SY.signal [1,2,3,4,5]>>>let s2 = SY.signal [10,10,10,10,10]>>>let v2 = vector [s1,s1,s1]>>>prefix (comb21 (+)) v2<{3,6,9,12,15},{2,4,6,8,10},{1,2,3,4,5}>>>>prefixi (comb21 (+)) s2 v2<{13,16,19,22,25},{12,14,16,18,20},{11,12,13,14,15}>
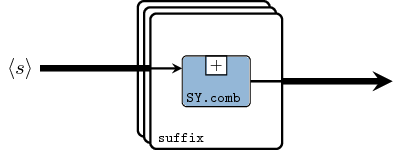
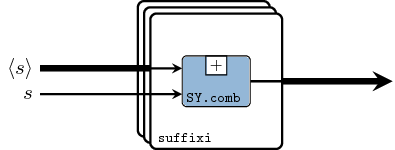
suffix :: (b -> b -> b) -> Vector b -> Vector b Source #
suffix peforms the parallel suffix operation on a vector.
Equivalent process networks are constructed if processes are passed
as arguments.
Similar to reduce and reducei, two versions suffix and
suffixi are provided.
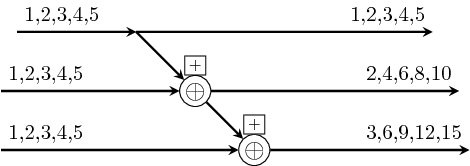
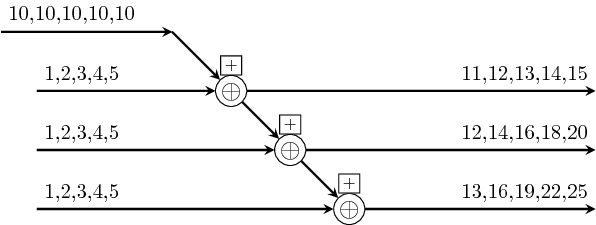
>>>let v1 = vector [1,2,3,4,5]>>>suffix (+) v1<1,3,6,10,15>>>>let s1 = SY.signal [1,2,3,4,5]>>>let s2 = SY.signal [10,10,10,10,10]>>>let v2 = vector [s1,s1,s1]>>>suffix (comb21 (+)) v2<{1,2,3,4,5},{2,4,6,8,10},{3,6,9,12,15}>>>>suffixi (comb21 (+)) s2 v2<{11,12,13,14,15},{12,14,16,18,20},{13,16,19,22,25}>
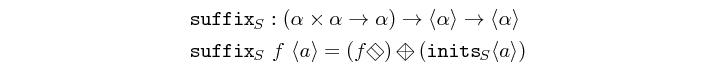
Arguments
| :: Vector (a -> a) | vector of functions |
| -> a | input |
| -> a | output |
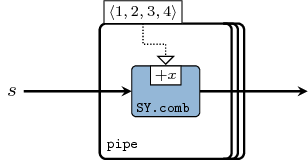
pipe creates a pipeline of functions from a vector. pipe
simply instantiates the =<<= atom whereas pipeX instantiate
their omologi from the ForSyDe.Atom.Skel module (see
pipe2).
OBS: the pipelining is done in the order dictated by the function composition operator: from right to left.
Constructors: pipe[1-4].
>>>let v1 = vector [(+1),(+1),(+1)]>>>S.pipe v1 14>>>let s1 = SY.signal [1,2,3,4]>>>let v2 = vector [1,2,3,4]>>>S.pipe1 (\x -> comb11 (+x)) v2 s1{11,12,13,14}

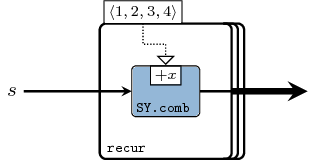
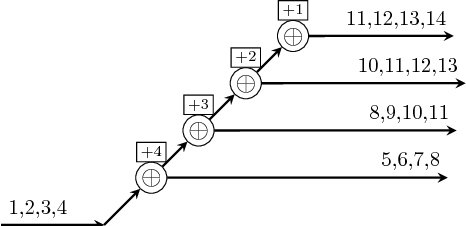
recur creates a systolic array from a vector of
functions. Just like pipe and pipeX, there exists a raw
recur version with an infix operator =/=, and the enhanced
recurX which is meant for systematic partial application of a
function on an arbitrary number of vectors until the desired vector
of functions is obtained.
Constructors: (=/=), recur, recuri, recur[1-4][1-4].
>>>let v1 = vector [(+1),(+1),(+1)]>>>recur v1 1<4,3,2>>>>recuri v1 1<4,3,2,1>>>>let s1 = SY.signal [1,2,3,4]>>>let v2 = vector [1,2,3,4]>>>recur1 (\x -> comb11 (+x)) v2 s1<{11,12,13,14},{10,11,12,13},{8,9,10,11},{5,6,7,8}>
Arguments
| :: (a2 -> a1 -> a -> a -> a) |
|
| -> Vector (Vector a2) | fills in the first argument in the function above |
| -> Vector (Vector a1) | fills in the second argument in the function above |
| -> Vector a | first input vector (e.g. of signals) |
| -> Vector a | second input vector (e.g. of signals) |
| -> Vector a | output |
cascade creates a "cascading mesh" as a result of piping a
vector into a vector of recur arrays.
Constructors: cascade, cascade[1-4].
>>>let v1 = vector [1,2,3,4]>>>cascade (+) v1 v1<238,119,49,14>>>>let s1 = SY.signal [1,2,3,4]>>>let vs = vector [s1, s1, s1]>>>cascade (comb21 (+)) vs vs<{20,40,60,80},{10,20,30,40},{4,8,12,16}>>>>let vv = vector [vector [1,-1,1], vector [-1,1,-1], vector [1,-1,1] ]>>>cascade1 (\x -> comb21 (\y z-> x*(y+z))) vv vs vs<{16,32,48,64},{8,16,24,32},{-2,-4,-6,-8}>
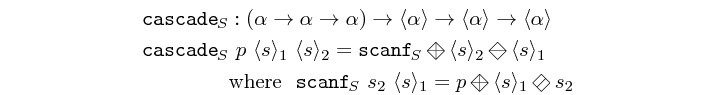


Arguments
| :: (a2 -> a1 -> a -> a -> a) |
|
| -> Vector (Vector a2) | fills in the first argument in the function above |
| -> Vector (Vector a1) | fills in the second argument in the function above |
| -> Vector a | first input vector (e.g. of signals) |
| -> Vector a | second input vector (e.g. of signals) |
| -> Vector (Vector a) | output, a 2D vector |
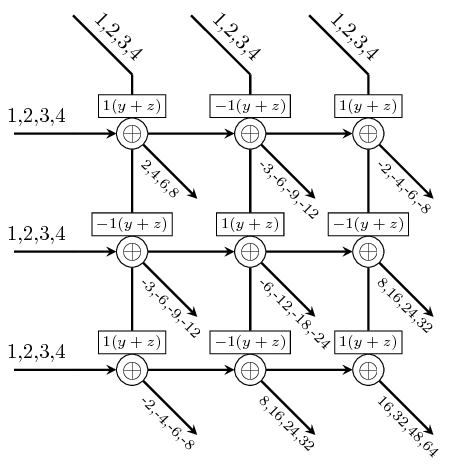
mesh creates a 2D systolic array as a result of piping a vector
into a vector of 1D systolic arrays.
Constructors: mesh, mesh[1-4].
>>>let v1 = vector [1,2,3,4]>>>mesh (+) v1 v1<<238,119,49,14>,<119,70,35,13>,<49,35,22,11>,<14,13,11,8>>>>>let s1 = SY.signal [1,2,3,4]>>>let vs = vector [s1, s1, s1]>>>mesh (comb21 (+)) vs vs<<{20,40,60,80},{10,20,30,40},{4,8,12,16}>,<{10,20,30,40},{6,12,18,24},{3,6,9,12}>,<{4,8,12,16},{3,6,9,12},{2,4,6,8}>>>>>let vv = vector [vector [1,-1,1], vector [-1,1,-1], vector [1,-1,1]]>>>mesh1 (\x -> comb21 (\y z-> x*(y+z))) vv vs vs<<{16,32,48,64},{8,16,24,32},{-2,-4,-6,-8}>,<{8,16,24,32},{-6,-12,-18,-24},{-3,-6,-9,-12}>,<{-2,-4,-6,-8},{-3,-6,-9,-12},{2,4,6,8}>>


Queries
Queries return various information about a vector. They are also built as skeletons.
length :: Num p => Vector a -> p Source #
returns the number of elements in a value.
>>>length $ vector [1,2,3,4,5]5
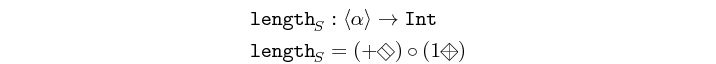
index :: Vector a2 -> Vector Int Source #
returns a vector with the indexes from another vector.
>>>index $ vector [1,1,1,1,1,1,1]<1,2,3,4,5,6,7>
Generators
Generators are specific applications of the prefix or suffix skeletons.
fanout :: t -> Vector t Source #
fanout repeats an element. As a process network it distributes
the same value or signal to all the connected processes down the
line. Depending on the target platform and the refinement decisions
involved, it may be interpreted in the following implementations:
- global or shared memory in case of a massively parallel platform (e.g. GPU)
- a (static) memory or cache location in memory-driven architectures (e.g. CPU)
- a fanout in case of a HDL system
- a broadcast in case of a distributed system
Permutators
Permutators perform operations on the very structure of vectors, and make heavy use of the vector constructors.
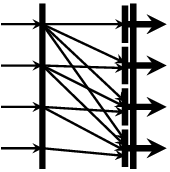
inits :: Vector a -> Vector (Vector a) Source #
creates a vector of all the initial segments in a vector.
>>>inits $ vector [1,2,3,4,5]<<1>,<1,2>,<1,2,3>,<1,2,3,4>,<1,2,3,4,5>>
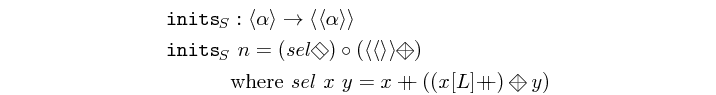
tails :: Vector a -> Vector (Vector a) Source #
creates a vector of all the final segments in a vector.
>>>tails $ vector [1,2,3,4,5]<<1,2,3,4,5>,<2,3,4,5>,<3,4,5>,<4,5>,<5>>
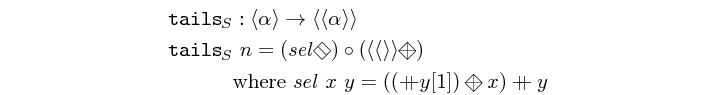
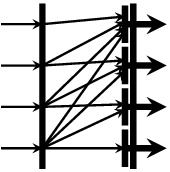
init :: Vector a -> Vector a Source #
Returns the initial segment of a vector.
>>>init $ vector [1,2,3,4,5]<1,2,3,4>
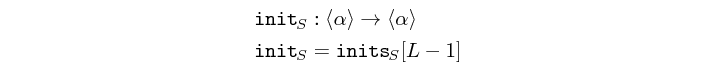
tail :: Vector a -> Vector a Source #
Returns the tail of a vector.
>>>tail $ vector [1,2,3,4,5]<2,3,4,5>
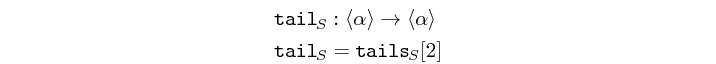
concat :: Vector (Vector a) -> Vector a Source #
concatenates a vector of vectors.
>>>concat $ vector [vector[1,2,3,4], vector[5,6,7]]<1,2,3,4,5,6,7>
reverse :: Vector a -> Vector a Source #
reverses the elements in a vector.
>>>reverse $ vector [1,2,3,4,5]<5,4,3,2,1>
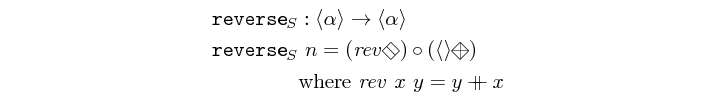

group :: Int -> Vector a -> Vector (Vector a) Source #
groups a vector into sub-vectors of n elements.
>>>group 3 $ vector [1,2,3,4,5,6,7,8]<<1,2,3>,<4,5,6>,<7,8>>
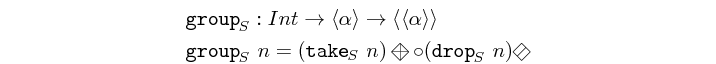

shiftr :: Vector a -> a -> Vector a Source #
right-shifts a vector with an element.
>>>vector [1,2,3,4] `shiftr` 8<8,1,2,3>
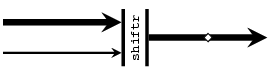
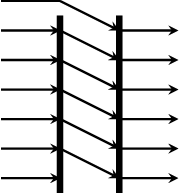
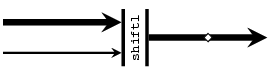
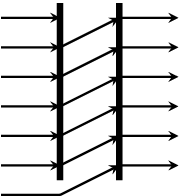
shiftl :: Vector a -> a -> Vector a Source #
left-shifts a vector with an element.
>>>vector [1,2,3,4] `shiftl` 8<2,3,4,8>
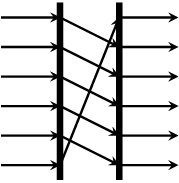
rotr :: Vector a -> Vector a Source #
rotates a vector to the right.
>>>rotr $ vector [1,2,3,4]<4,1,2,3>
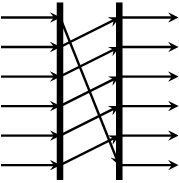
rotl :: Vector a -> Vector a Source #
rotates a vector to the left.
>>>rotl $ vector [1,2,3,4]<2,3,4,1>
rotate :: Int -> Vector a -> Vector a Source #
rotates a vector to the left or to the right depending on the index:
(> 0): rotates the vector right with the corresponding number of positions.(= 0): does not modify the vector.(< 0): rotates the vector left with the corresponding number of positions.
take :: Int -> Vector a -> Vector a Source #
takes the first n elements of a vector.
>>>take 5 $ vector [1,2,3,4,5,6,7,8,9]<1,2,3,4,5>
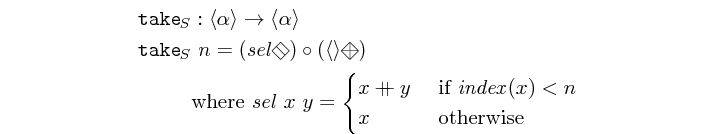
drop :: Int -> Vector a -> Vector a Source #
drops the first n elements of a vector.
>>>drop 5 $ vector [1,2,3,4,5,6,7,8,9]<6,7,8,9>
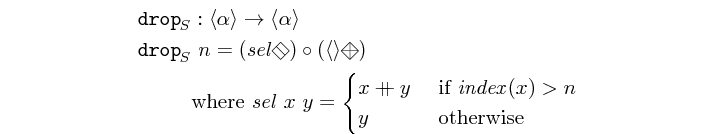
takeWhile :: (a -> Bool) -> Vector a -> Vector a Source #
takes the first elements in a vector until the first element that does not fulfill a predicate.
>>>takeWhile (<5) $ vector [1,2,3,4,5,6,7,8,9]<1,2,3,4>
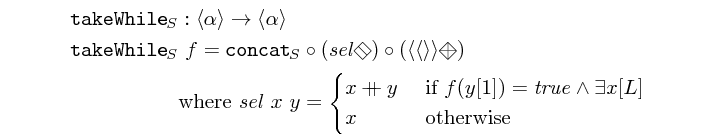
filterIdx :: (Int -> Bool) -> Vector a -> Vector a Source #
returns a vector containing only the elements of another vector whose index satisfies a predicate.
>>>filterIdx (\x -> x `mod` 3 == 0) $ vector [0,1,2,3,4,5,6,7,8,9]<2,5,8>
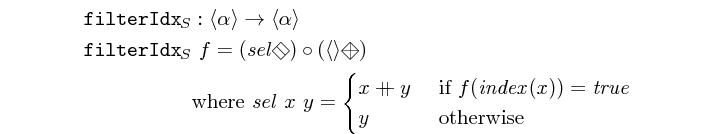

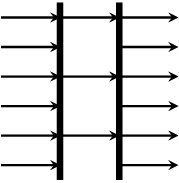
does a stride-selection on a vector.
>>>stride 1 3 $ vector [1,2,3,4,5,6,7,8,9]<1,4,7>
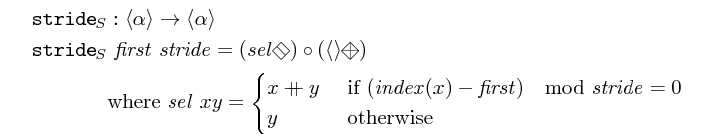


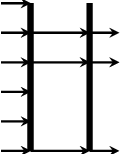
get :: Int -> Vector a -> Maybe a Source #
returns the n-th element in a vector, or Nothing if n > l.
>>>get 3 $ vector [1,2,3,4,5]Just 3
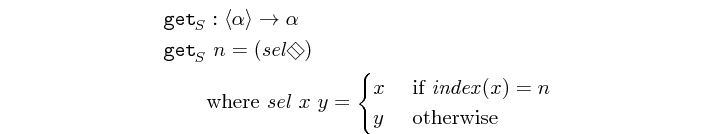
selects the elements in a vector at the incexes contained by another vector.
The following versions of this skeleton are available, the number
suggesting how many nested vectors it is operating upon: gather[1-5]
>>>let ix = vector [vector [1,3,4], vector [3,5,1], vector [5,8,9]]>>>let v = vector [11,12,13,14,15]>>>gather2 ix v<<Just 11,Just 13,Just 14>,<Just 13,Just 15,Just 11>,<Just 15,Nothing,Nothing>>


the same as gather1 but with flipped arguments
The following versions of this skeleton are available, the number suggesting how many nested vectors it is operating upon.
(<@>), (<<@>>), (<<<@>>>), (<<<<@>>>>), (<<<<<@>>>>>),
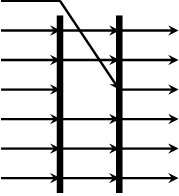
replace :: Int -> a -> Vector a -> Vector a Source #
replaces the n-th element in a vector with another.
>>>replace 5 15 $ vector [1,2,3,4,5,6,7,8,9]<1,2,3,4,15,6,7,8,9>
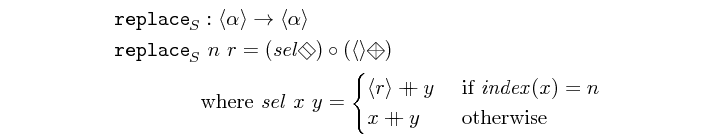

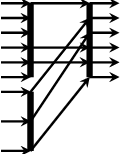
scatter :: Vector Int -> Vector a -> Vector a -> Vector a Source #
scatters the elements in a vector based on the indexes contained by another vector.
>>>scatter (vector [2,4,5]) (vector [0,0,0,0,0,0,0,0]) (vector [1,1,1])<0,1,0,1,1,0,0,0>
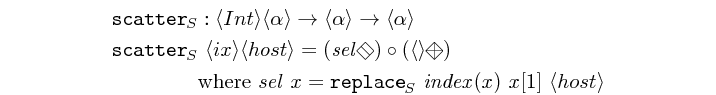

Interfaces
Arguments
| :: MoC e | |
| => Vector ((Vector a -> Vector a -> Vector a) -> Fun e (Vector a) (Fun e (Vector a) (Ret e (Vector a)))) | vector of MoC-specific context wrappers for the function
|
| -> Vector (Stream (e a)) | input vector of signals |
| -> Stream (e (Vector a)) | output signal of vectors |
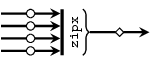
zipx is a template skeleton for "zipping" a vector of
signals. It synchronizes all signals (of the same MoC) in a vector
and outputs one signal with vectors of the synced values. For each
signal in the input vector it requires a function which
translates a partition of events (see ForSyDe.Atom.MoC) into
sub-vectors.
There exist helper instances of the zipx skeleton interface for
all supported MoCs.
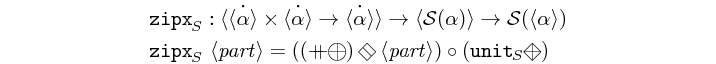
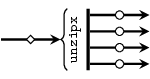
unzipx :: MoC e => (Vector a -> Vector (Ret e a)) -> Integer -> Stream (e (Vector a)) -> Vector (Stream (e a)) Source #
unzipx is a template skeleton to unzip a signal carrying
vectors into a vector of multiple signals. It required a function
that splits a vector of values into a vector of event partitions
belonging to output signals. Unlike zipx, it also requires the
number of output signals. The reason for this is that it is
impossible to determine the length of the output vector without
"sniffing" the content of the input events, which is out of the
scope of skeletons and may lead to unsafe behavior. The length of
the output vector is needed in order to avoid infinite recurrence.
There exist helper instances of the unzipx skeleton interface for
all supported MoCs.