| Copyright | (c) George Ungureanu 2015-2017 |
|---|---|
| License | BSD-style (see the file LICENSE) |
| Maintainer | ugeorge@kth.se |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | Safe |
| Language | Haskell2010 |
| Extensions |
|
ForSyDe.Atom.MoC
Description
This module exports the core entities of the MoC layer: interfaces for atoms and process constructors as patterns of atoms. It does NOT export any implementation or instance of any specific MoC. For an overview about atoms, layers and patterns, please refer to the ForSyDe.Atom module documentation, and for an overview of the MoC layer entities refer to the MoC layer section.
The MoCs currently implemented in ForSyDe-Atom are shown in the instances section, and they can be used in designs by importing their respective modules:
IMPORTANT!!! see the naming convention rules on how to interpret, use and develop your own constructors.
Synopsis
- class Applicative e => MoC e where
- delay :: MoC e => Stream (e a) -> Stream (e a) -> Stream (e a)
- (-&>-) :: MoC e => Stream (e a) -> Stream (e a) -> Stream (e a)
- comb22 :: MoC e => Fun e a1 (Fun e a2 (Ret e b1, Ret e b2)) -> Stream (e a1) -> Stream (e a2) -> (Stream (e b1), Stream (e b2))
- reconfig22 :: MoC e => Stream (e (Fun e a1 (Fun e a2 (Ret e b1, Ret e b2)))) -> Stream (e a1) -> Stream (e a2) -> (Stream (e b1), Stream (e b2))
- state22 :: MoC e => Fun e st1 (Fun e st2 (Fun e a1 (Fun e a2 (Ret e st1, Ret e st2)))) -> (Stream (e st1), Stream (e st2)) -> Stream (e a1) -> Stream (e a2) -> (Stream (e st1), Stream (e st2))
- stated22 :: MoC e => Fun e st1 (Fun e st2 (Fun e a1 (Fun e a2 (Ret e st1, Ret e st2)))) -> (Stream (e st1), Stream (e st2)) -> Stream (e a1) -> Stream (e a2) -> (Stream (e st1), Stream (e st2))
- moore22 :: MoC e => Fun e st (Fun e a1 (Fun e a2 (Ret e st))) -> Fun e st (Ret e b1, Ret e b2) -> Stream (e st) -> Stream (e a1) -> Stream (e a2) -> (Stream (e b1), Stream (e b2))
- mealy22 :: MoC e => Fun e st (Fun e a1 (Fun e a2 (Ret e st))) -> Fun e st (Fun e a1 (Fun e a2 (Ret e b1, Ret e b2))) -> Stream (e st) -> Stream (e a1) -> Stream (e a2) -> (Stream (e b1), Stream (e b2))
- ctxt22 :: (ctx, ctx) -> (ctx, ctx) -> (a1 -> a2 -> (b1, b2)) -> (ctx, a1 -> (ctx, a2 -> ((ctx, b1), (ctx, b2))))
- warg :: c -> (a -> b) -> (c, a -> b)
- wres :: p -> b -> (p, b)
- (-*<) :: MoC e => Stream (e (Ret e b1, Ret e b2)) -> (Stream (e b1), Stream (e b2))
Atoms
class Applicative e => MoC e where Source #
This is a type class defining interfaces for the MoC layer atoms. Each model of computation exposes its tag system through a unique event type which is an instance of this class, defining \( T \times V \).
To express all possible MoCs which can be described using a tagged signal model we need to capture the most general form of their atoms. This means that under the same interface we need to describe atoms with different execution regimes. Recall that atoms are in principle applicative functors which act upon one input signal at a time and partially apply functions. Depending on the execution regime, these function might or might not need additional parameters to determine the behavior for evaluating each argument. These additional parameters we call, in loose terms, as the execution context.
- execution context
- Additional information which, paired with a function, completely determines the behavior of a MoC atom (i.e. process).
The left-hand side expression above shows the most general notation used to describe a function with n inputs of (possibly different) types \(\alpha\) and m outputs of (possibly different) types \(\beta\) executed in context \(\Gamma\). The right-hand side expression shows that in ForSyDe-Atom context is associated with each and every argument in order to enable the applicative mechanisms. Depending on the MoC, \(\breve\alpha\) would translate to:
One example of execution context is the consumption and production
rates for data flow MoCs (e.g. SDF). In this
case the passed functions are defined over "sequences" or
"partitions" of events, i.e. groupings of events with the same
partial order in relation to a process firing.
While in the example above the execution context can be extracted
from the type information, working with type-level parameters is
not a trivial task in Haskell, especially if we want to describe a
general and extensible type class. This is why we have chosen a
pragmatic approach in implementing the MoC class:
- any (possible) Cartesian product which denotes a partition of \(\alpha\) is represented using a recursive type, namely a list \([\alpha]\).
- as the execution context cannot (or can hardly) be extracted from
the recursive type, in the most general case we pass both context
and argument as a pair (see each instance in particular). To
aid in pairing contexts with each argument in a function, the
general purpose
ctxtutilities are provided (seectxt22). - this artifice is masked using the generic type families
FunandRet.
Associated Types
This is a type family alias \(^1\) for a context-bound function
passed as an argument to a MoC atom. It can be regarded as an
enhanced -> type operator, specific to each MoC.
\(^1\) While hiding the explicit definition of arguments, this implementation choice certainly has its advantages in avoiding unnecessary or redundant type constructors (see version 0.1.1 and prior). Aliases are replaced at compile time, thus not affecting run-time performance.
Methods
(-.-) :: Fun e a b -> Stream (e a) -> Stream (e b) infixl 5 Source #
The func atom is mapping a function on values (in the
presence of a context) to a signal, i.e. stream of tagged
events. As ForSyDe deals with determinate, functional
processes, this atom defines the (only) behavior of a process
in rapport to one input signal [Lee98].
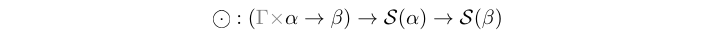
(-*-) :: Stream (e (Fun e a b)) -> Stream (e a) -> Stream (e b) infixl 5 Source #
The sync atom synchronizes two signals, one carrying
functions on values (in the presence of a context), and the other
containing values. During the synchronization it applies the
function(s) carried by the former signal on the values carried by
the latter. This atom defines a relation between two signals
[Lee98].
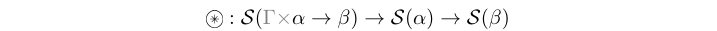
(-*) :: Stream (e (Ret e b)) -> Stream (e b) infixl 3 Source #
Artificial utility which drops the context and/or partitioning yielding a clean signal type.
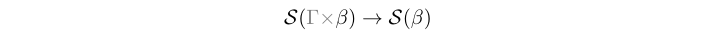
(-<-) :: Stream (e a) -> Stream (e a) -> Stream (e a) infixl 3 Source #
The pre atom prepends the prefix of the left signal operand
(i.e. the first event in timed MoCs, or the first n events in
untimed MoCs) at the beginning of the right signal operand
\(^1\). This atom is necessary to ensure complete partial order
of a signal and assures the least upper bound necessary for
example in the evaluation of feedback loops
[Lee98].
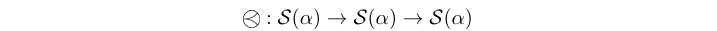
\(^1\) this atom acts like the pre operator in the synchronous
language Lustre [Halbwachs91],
and for timed MoCs it behaves the same. For untimed MoCs though,
the length of the prefix of a signal is assumed to be the length
of a signal, since the API does not provide any other means to
pass n as a parameter.
(-&-) :: Stream (e a) -> Stream (e a) -> Stream (e a) infixl 3 Source #
The phi atom manipulates the tags in a signal in a
restrictive way which preserves monotonicity and continuity
in a process [Lee98], namely by
“phase-shifting” all tags in a signal with the appropriate metric
corresponding to each MoC. Thus it preserves the characteristic
function intact [Sander04].
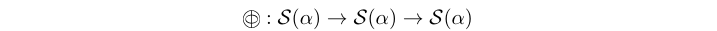
The metric unit used for phase shifting is inferred from the prefix of the left signal operand, while right signal operand is the one being manipulated.
Instances
| MoC SY Source # | Implenents the execution semantics for the SY MoC atoms. |
Defined in ForSyDe.Atom.MoC.SY.Core Methods (-.-) :: Fun SY a b -> Stream (SY a) -> Stream (SY b) Source # (-*-) :: Stream (SY (Fun SY a b)) -> Stream (SY a) -> Stream (SY b) Source # (-*) :: Stream (SY (Ret SY b)) -> Stream (SY b) Source # (-<-) :: Stream (SY a) -> Stream (SY a) -> Stream (SY a) Source # (-&-) :: Stream (SY a) -> Stream (SY a) -> Stream (SY a) Source # | |
| MoC SDF Source # | Implenents the SDF semantics for the MoC atoms. |
Defined in ForSyDe.Atom.MoC.SDF.Core Methods (-.-) :: Fun SDF a b -> Stream (SDF a) -> Stream (SDF b) Source # (-*-) :: Stream (SDF (Fun SDF a b)) -> Stream (SDF a) -> Stream (SDF b) Source # (-*) :: Stream (SDF (Ret SDF b)) -> Stream (SDF b) Source # (-<-) :: Stream (SDF a) -> Stream (SDF a) -> Stream (SDF a) Source # (-&-) :: Stream (SDF a) -> Stream (SDF a) -> Stream (SDF a) Source # | |
| MoC DE Source # | Implenents the execution semantics for the DE MoC atoms. |
Defined in ForSyDe.Atom.MoC.DE.Core Methods (-.-) :: Fun DE a b -> Stream (DE a) -> Stream (DE b) Source # (-*-) :: Stream (DE (Fun DE a b)) -> Stream (DE a) -> Stream (DE b) Source # (-*) :: Stream (DE (Ret DE b)) -> Stream (DE b) Source # (-<-) :: Stream (DE a) -> Stream (DE a) -> Stream (DE a) Source # (-&-) :: Stream (DE a) -> Stream (DE a) -> Stream (DE a) Source # | |
| MoC CT Source # | Implenents the execution semantics for the CT MoC atoms. |
Defined in ForSyDe.Atom.MoC.CT.Core Methods (-.-) :: Fun CT a b -> Stream (CT a) -> Stream (CT b) Source # (-*-) :: Stream (CT (Fun CT a b)) -> Stream (CT a) -> Stream (CT b) Source # (-*) :: Stream (CT (Ret CT b)) -> Stream (CT b) Source # (-<-) :: Stream (CT a) -> Stream (CT a) -> Stream (CT a) Source # (-&-) :: Stream (CT a) -> Stream (CT a) -> Stream (CT a) Source # | |
Patterns
The atom patterns of the MoC layer are in fact process constructors. Check the naming convention of the API in the page description.
delay :: MoC e => Stream (e a) -> Stream (e a) -> Stream (e a) Source #
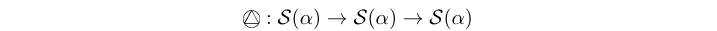
The delay process provides both initial token(s) and shifts the
phase of the signal. In other words, it "delays" a signal with
one or several events.
(-&>-) :: MoC e => Stream (e a) -> Stream (e a) -> Stream (e a) infixl 3 Source #
Infix variant for delay.
Arguments
| :: MoC e | |
| => Fun e a1 (Fun e a2 (Ret e b1, Ret e b2)) | combinational function (*) |
| -> Stream (e a1) | first input signal |
| -> Stream (e a2) | second input signal |
| -> (Stream (e b1), Stream (e b2)) | two output signals |
(*) to be read a1 -> a2 -> (b1, b2) where each
argument may be wrapped along with a context.
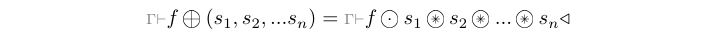
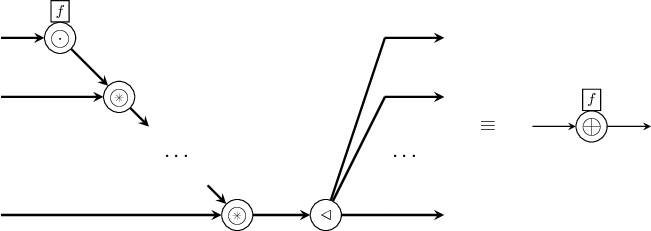
The comb processes synchronizes multiple input signals and maps
combinatorial functions on the values they carry.
This module exports constructors of type comb[1-8][1-4].
Arguments
| :: MoC e | |
| => Stream (e (Fun e a1 (Fun e a2 (Ret e b1, Ret e b2)))) | signal carrying functions (*) |
| -> Stream (e a1) | first input signal |
| -> Stream (e a2) | second input signal |
| -> (Stream (e b1), Stream (e b2)) | two output signals |
(*) to be read a1 -> a2 -> (b1, b2) where each
argument may be wrapped along with a context.
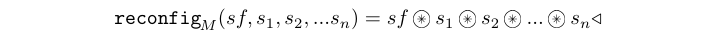
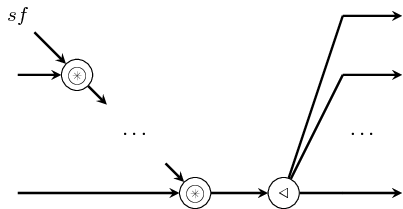
The reconfig processes constructs adaptive processes, whose
functional behavior "changes in time". Its first input is a signal
carrying functions which is synchronized with all the other input
signals. The output signal carry the results of mapping those
functions at each synchronization/firing point.
This library exports constructors of type reconfig[1-8][1-4].
Arguments
| :: MoC e | |
| => Fun e st1 (Fun e st2 (Fun e a1 (Fun e a2 (Ret e st1, Ret e st2)))) | next state function (*) |
| -> (Stream (e st1), Stream (e st2)) | initial state(s) (**) |
| -> Stream (e a1) | first input signal |
| -> Stream (e a2) | second input signal |
| -> (Stream (e st1), Stream (e st2)) | output signals mirroring the next state(s). |
(*) meaning st1 -> st2 -> a1 -> a2 -> (st1,st2)
where each argument may be wrapped along with a context.
(**) inferred from the prefixes of the signals passed
as arguments. See the documentation for -<- for an explanation.
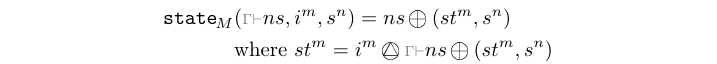
The state processes generate process networks corresponding to a
simple state machine with "un-latched" outputs like in the graph
above. In other words, the process starts with a state transition
and outputs the next state as the first event.
This library exports constructors of type state[1-4][1-4].
Arguments
| :: MoC e | |
| => Fun e st1 (Fun e st2 (Fun e a1 (Fun e a2 (Ret e st1, Ret e st2)))) | next state function (*) |
| -> (Stream (e st1), Stream (e st2)) | initial state(s) (**) |
| -> Stream (e a1) | first input signal |
| -> Stream (e a2) | second input signal |
| -> (Stream (e st1), Stream (e st2)) | output signals mirroring the next state(s). |
(*) meaning st1 -> st2 -> a1 -> a2 -> (st1,st2)
where each argument may be wrapped along with a context.
(**) inferred from the prefixes of the signals passed
as arguments. See the documentation for -<- for an explanation.
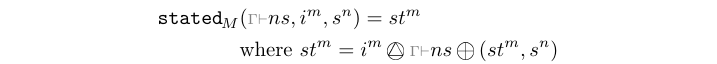
The stated processes generate process networks corresponding to a
simple state machine with "latched" outputs like in the graph
above. As compared to state22, this process outputs the current
state, and the state transition is observed from the second
evaluation onwards. There exists a variant with 0 input signals, in
which case the process is a signal generator.
This library exports constructors of type stated[0-4][1-4].
Arguments
| :: MoC e | |
| => Fun e st (Fun e a1 (Fun e a2 (Ret e st))) | next state function (*) |
| -> Fun e st (Ret e b1, Ret e b2) | output decoder (**) |
| -> Stream (e st) | initial state (***) |
| -> Stream (e a1) | first input signal |
| -> Stream (e a2) | second input signal |
| -> (Stream (e b1), Stream (e b2)) | output signals |
(*) meaning st -> a1 -> a2 -> st where each
argument may be wrapped along with a context.
(**) meaning st -> (b1, b2) where each argument
may be wrapped along with a context.
(***) inferred from the prefixes of the signals passed
as arguments. See the documentation for -<- for an explanation.
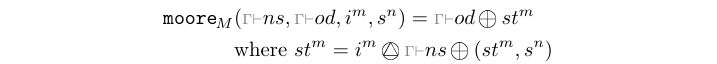
The moore processes model Moore state machines.
This library exports constructors of type moore[1-4][1-4].
Arguments
| :: MoC e | |
| => Fun e st (Fun e a1 (Fun e a2 (Ret e st))) | next state function (*) |
| -> Fun e st (Fun e a1 (Fun e a2 (Ret e b1, Ret e b2))) | output decoder (**) |
| -> Stream (e st) | initial state (***) |
| -> Stream (e a1) | first input signal |
| -> Stream (e a2) | second input signal |
| -> (Stream (e b1), Stream (e b2)) | output signals |
(*) meaning st -> a1 -> a2 -> st where each
argument may be wrapped along with a context.
(**) meaning st -> a1 -> a2 -> (b1, b2) where
each argument may be wrapped along with a context.
(***) inferred from the prefixes of the signals passed
as arguments. See the documentation for -<- for an explanation.
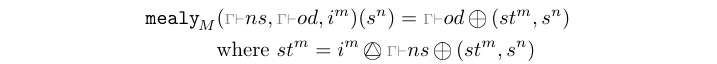
The mealy processes model Mealy state machines.
This library exports constructors of type mealy[1-4][1-4].
Utilities
Arguments
| :: (ctx, ctx) | argument contexts (e.g. consumption rates in SDF) |
| -> (ctx, ctx) | result contexts (e.g. production rates in SDF) |
| -> (a1 -> a2 -> (b1, b2)) | function on values/partitions of values |
| -> (ctx, a1 -> (ctx, a2 -> ((ctx, b1), (ctx, b2)))) | context-wrapped form of the previous function |
Wraps a function with the context needed by some MoCs for their constructors (e.g. rates in SDF).
This library exports wrappers of type ctxt[1-8][1-4].
warg :: c -> (a -> b) -> (c, a -> b) Source #
Attaches a context parameter to a function argument (e.g
consumption rates in SDF). Used as kernel function in defining
e.g. ctxt22.