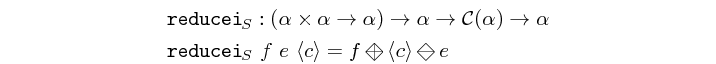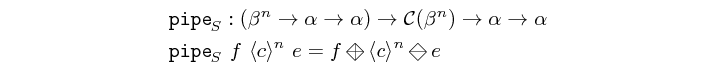| Copyright | (c) George Ungureanu KTH/ICT/ESY 2015 |
|---|---|
| License | BSD-style (see the file LICENSE) |
| Maintainer | ugeorge@kth.se |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | Safe |
| Language | Haskell2010 |
| Extensions | PostfixOperators |
ForSyDe.Atom.Skel
Contents
Description
This module defines the Skeleton layer, and is concerned in modeling the aspects of inherent potential for parallelism in CPS. Its formal foundation is the theory of algorithmic skeletons [Skillicorn05], and it adapts it according to the atom approach. For more on our approach, and how it fits into the layered framework, please consult [Ungureanu20a]
This library is concerned in modeling the theoretical aspects as faithfully as possible using a shallow DSL, and not necessarily reaping the benefits of parallelization directly in simulations. The latter would require further engineering and the modeling concepts are likely to be lost the process. Instead most of the atom and pattern formulations in this module and sub-modules might not be the most efficient implementations for the given functionality, but rather expose the fundamental properties which can be further exploited in design processes. Of these properties our special interest lies in the factorization theorem (see [Skillicorn05], [Gorlatch03]), which sets the framework for any skeleton to be further transformed into semantically-equivalent forms, more appropriate for execution on various platforms.
Similar to other layer libraries, this module defines only atoms and patterns as type class methods, i.e. "shells" which are not loaded with any semantics. It is unlikely that the user will need this API, but rather load any of its sub-modules directly:
- ForSyDe.Atom.Skel.Vector is a shallow interpretation of the vector category, susceptible to algorithmic skeletons. It defines a large library of patterns commonly used in designs.
- ForSyDe.Atom.Skel.FastVector is an un-official alternative to
ForSyDe.Atom.Skel.Vector meant for simulations of large data which is
likely to become too cumbersome. It does not use atoms, but rather it wraps
native Haskell types into
newtypewrappers and uses Prelude functions internally. The API tries to copy that of ForSyDe.Atom.Skel.Vector so that switching betwen libraries can be made seamlessly just by changing the import.
Synopsis
- class Functor c => Skeleton c where
- farm22 :: Skeleton c => (a1 -> a2 -> (b1, b2)) -> c a1 -> c a2 -> (c b1, c b2)
- reduce :: Skeleton c => (a -> a -> a) -> c a -> a
- reducei :: Skeleton c => (a -> a -> a) -> a -> c a -> a
- pipe :: Skeleton c => c (a -> a) -> a -> a
- pipe2 :: Skeleton c => (a1 -> a2 -> a -> a) -> c a1 -> c a2 -> a -> a
Atoms
class Functor c => Skeleton c where Source #
Class containing all the Skeleton layer atoms.
This class is instantiated by a set of categorical types, i.e. types which describe an inherent potential for being evaluated in parallel. Skeletons are patterns from this layer. All skeletons can be described as composition of the three atoms below. This possible due to an existing theorem in the categorical type theory, also called the Bird-Merteens formalism:
- factorization
- A function on a categorical type is an algorithmic skeleton (i.e. catamorphism) iff it can be represented in a factorized form, i.e. as a map composed with a reduce.
Methods
(=.=) :: (a -> b) -> c a -> c b infixl 4 Source #
Atom which maps a function on each element of a structure (i.e. categorical type), defined as:
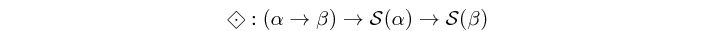
(=*=) :: c (a -> b) -> c a -> c b infixl 4 Source #
Atom which applies the functions contained by as structure (i.e. categorical type), on the elements of another structure, defined as:
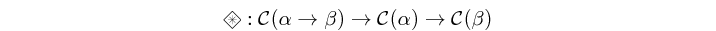
(=\=) :: (a -> a -> a) -> c a -> a infixl 2 Source #
Atom which reduces a structure to an element based on an associative function, defined as:
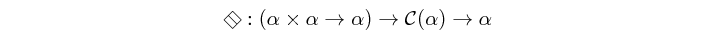
Arguments
| :: c (a -> a) | vector of functions |
| -> a | kernel element |
| -> a | result |
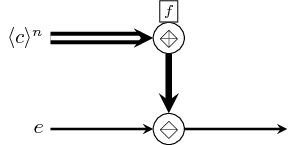
Skeleton which pipes an element through all the functions contained by a structure. This is not an atom. It has an implicit definition which might be augmented by instances of this class to include edge cases.
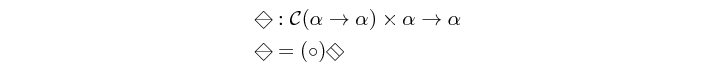
As the composition operation is not associative, we cannot treat pipe as a true
reduction. However it can still be exploited in parallel since it exposes another
type of parallelism: time parallelism.
Returns the first element in a structure. This is not an atom. It has an implicit definition which might be replaced by instances of this class with a more efficient implementation.
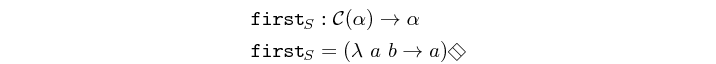
Returns the last element in a structure. This is not an atom. It has an implicit definition which might be replaced by instances of this class with a more efficient implementation.
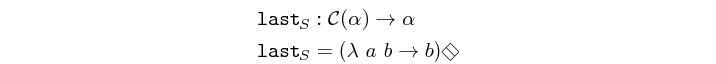
Skeleton constructors
Patterns of in the skeleton layer are provided, like all other patterns in
ForSyDe-Atom, as constructors. If the layer below this one is the
MoC layer, i.e. the functions taken as arguments are
processes, then these skeletons can be regarded as process network constructors,
as the structures created are process networks with inherent potential for
parallel implementation.
farm22 :: Skeleton c => (a1 -> a2 -> (b1, b2)) -> c a1 -> c a2 -> (c b1, c b2) Source #
farm maps a function on a vector. It is the embodiment of the
map homomorphism, and its naming is inspired from the pattern
predominant in HPC. Indeed, if we consider the layer below as being
the MoC layer (i.e. the passed functions are
processes), the resulting structure could be regarded as a "farm of
data-parallel processes".
Constructors: farm[1-8][1-4].
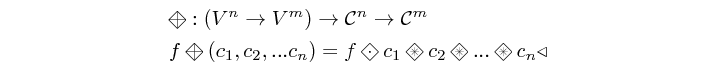

Arguments
| :: Skeleton c | |
| => (a -> a -> a) | associative function (*) |
| -> c a | structure |
| -> a | reduced element |
Infix name for the =\= atom operator.
(*) if the operation is not associative then the network can be treated like a pipeline.
Arguments
| :: Skeleton c | |
| => (a -> a -> a) | associative function (*) |
| -> a | initial element of structure |
| -> c a | structure |
| -> a | reduced element |
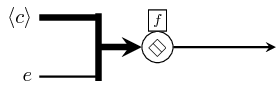
reducei is special case of reduce where an initial element is
specified outside the reduced vector. It is implemented as a
pipe with switched arguments, and the reduction function is
constrained to be associative. It is semantically equivalent to the
pattern depicted below.
(*) if the operation is not associative then the network is
semantically equivalent to pipe1 (see pipe2).