| Copyright | (c) George Ungureanu 2015-2016 |
|---|---|
| License | BSD-style (see the file LICENSE) |
| Maintainer | ugeorge@kth.se |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | Safe |
| Language | Haskell2010 |
ForSyDe.Atom.MoC.SY
Description
The SY library implements the atoms that operate according to the synchronous
reactive model of computation. This module also provides a set of helpers for
instantiating the MoC layer patterns described in the ForSyDe.Atom.MoC module as
meaningful synchronous process constructors.
This module exports a reduced SY language, where all processes are assumed to operate on the same clock rate. For an extended SY language of implicit multi-clock rate systems, check ForSyDe.Atom.MoC.SY.Clocked. Alternatively, this layer can be extended by explicitly wrapping a ForSyDe.Atom.ExB-like layer below it.
Useful pointers:
- ForSyDe.Atom contains general guidelines for using the API
- ForSyDe.Atom.MoC documents details about the internals of the MoC layer, the atoms and the basic structure of all process constructors as MoC patterns.
- ForSyDe.Atom.MoC.SY.Clocked contains an extended SY language of multi-rate clocked systems.
- the naming convention rules on how to interpret the function names based on their number of inputs and outputs.
Synopsis
- newtype SY a = SY {
- val :: a
- type Signal a = Stream (SY a)
- unit2 :: (a1, a2) -> (Signal a1, Signal a2)
- signal :: [a] -> Signal a
- readSignal :: Read a => String -> Signal a
- delay :: a -> Signal a -> Signal a
- comb22 :: (a1 -> a2 -> (b1, b2)) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- reconfig22 :: Signal (a1 -> a2 -> (b1, b2)) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- constant2 :: (b1, b2) -> (Signal b1, Signal b2)
- generate2 :: (b1 -> b2 -> (b1, b2)) -> (b1, b2) -> (Signal b1, Signal b2)
- stated22 :: (b1 -> b2 -> a1 -> a2 -> (b1, b2)) -> (b1, b2) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- state22 :: (b1 -> b2 -> a1 -> a2 -> (b1, b2)) -> (b1, b2) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- moore22 :: (st -> a1 -> a2 -> st) -> (st -> (b1, b2)) -> st -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- mealy22 :: (st -> a1 -> a2 -> st) -> (st -> a1 -> a2 -> (b1, b2)) -> st -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- toDE2 :: (Num t, Ord t, Eq t) => Signal t -> Signal a -> Signal b -> (SignalBase t a, SignalBase t b)
- toSDF2 :: Signal a -> Signal b -> (Signal a, Signal b)
- toSDF2' :: (Prod, Prod) -> Signal (Vector a) -> Signal (Vector b) -> (Signal a, Signal b)
- zipx :: Vector (Signal a) -> Signal (Vector a)
- unzipx :: Integer -> Signal (Vector a) -> Vector (Signal a)
- unzipx' :: Signal (Vector a) -> Vector (Signal a)
Synchronous (SY) event
Acording to the tagged signal model [Lee98] "two
events are synchronous if they have the same tag, and two signals are synchronous
if all events in one signal are synchronous to an event in the second signal and
vice-versa. A system is synchronous if every signals in the system is synchronous
to all the other signals in the system." The synchronous (SY) MoC defines no
notion of physical time, its tag system suggesting in fact the precedence among
events. In simpler words:
- The SY MoC
- is abstracting the execution semantics of a system where computation is assumed to perform instantaneously (with zero delay), at certain synchronization instants, when data is assumed to be available.
Below is a possible behavior in time of the input and the output signals of a SY process, to illustrate these semantics:
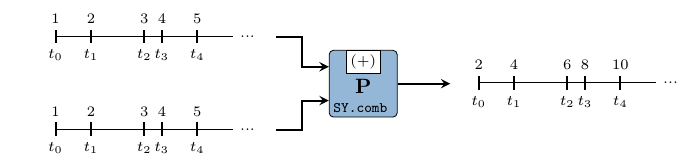
The SY tag system is derived directly from the Stream host.
Hence a SY Signal is isomorphic to an infinite list, where tags are implicitly
defined by the position of events in a signal: \(t_0\) corresponds with the event
at the head of a signal, \(t_1\) with the following event, etc... The only
explicit parameter passed to a SY event constructor is the value it carries (in
V). As such, we can state the following particularities:
- tags are implicit from the position in the
Stream, thus they are ignored in the type constructor. - the type constructor wraps only a value
- being a timed MoC, the order between events is interpreted as total.
- there is no need for an execution context and we can ignore the formatting of functions in ForSyDe.Atom.MoC, thus we can safely assume that \[ \Gamma\vdash\alpha\rightarrow\beta = \alpha\rightarrow\beta \]
The SY event. It defines a synchronous signal.
Instances
| Functor SY Source # | Allows for mapping of functions on a SY event. |
| Applicative SY Source # | Allows for lifting functions on a pair of SY events. |
| MoC SY Source # | Implenents the execution semantics for the SY MoC atoms. |
Defined in ForSyDe.Atom.MoC.SY.Core Methods (-.-) :: Fun SY a b -> Stream (SY a) -> Stream (SY b) Source # (-*-) :: Stream (SY (Fun SY a b)) -> Stream (SY a) -> Stream (SY b) Source # (-*) :: Stream (SY (Ret SY b)) -> Stream (SY b) Source # (-<-) :: Stream (SY a) -> Stream (SY a) -> Stream (SY a) Source # (-&-) :: Stream (SY a) -> Stream (SY a) -> Stream (SY a) Source # | |
| Read a => Read (SY a) Source # | Reads the value wrapped |
| Show a => Show (SY a) Source # | Shows the value wrapped |
| Plottable a => Plot (Signal a) Source # |
|
| type Ret SY b Source # | |
Defined in ForSyDe.Atom.MoC.SY.Core | |
| type Fun SY a b Source # | |
Defined in ForSyDe.Atom.MoC.SY.Core | |
Aliases & utilities
These are type synonyms and utilities provided for user convenience. They mainly concern the construction and usage of signals.
type Signal a = Stream (SY a) Source #
Type synonym for a SY signal, i.e. "an ordered stream of SY events"
unit2 :: (a1, a2) -> (Signal a1, Signal a2) Source #
Wraps a (tuple of) value(s) into the equivalent unit signal(s). A unit signal is a signal with one event, i.e. a singleton.
Provided helpers: unit, unit2, unit3, unit4.
readSignal :: Read a => String -> Signal a Source #
Reads a signal from a string. Like with the read function from
Prelude, you must specify the type of the signal.
>>>readSignal "{1,2,3,4,5}" :: Signal Int{1,2,3,4,5}
SY process constuctors
These are specific implementations of the atom patterns defined in ForSyDe.Atom.MoC.
Simple
The delay process "delays" a signal with one
event. Instantiates the delay pattern.
>>>let s = signal [1,2,3,4,5]>>>delay 0 s{0,1,2,3,4,5}

Arguments
| :: (a1 -> a2 -> (b1, b2)) | function on values |
| -> Signal a1 | first input signal |
| -> Signal a2 | second input signal |
| -> (Signal b1, Signal b2) | two output signals |
comb processes map combinatorial functions on signals and take care of
synchronization between input signals. It implements the comb pattern (see
comb22).
Constructors: comb[1-4][1-4].
>>>let s1 = signal [1..]>>>let s2 = signal [1,1,1,1,1]>>>comb11 (+1) s2{2,2,2,2,2}>>>comb22 (\a b-> (a+b,a-b)) s1 s2({2,3,4,5,6},{0,1,2,3,4})

Arguments
| :: Signal (a1 -> a2 -> (b1, b2)) | signal carrying functions |
| -> Signal a1 | first input signal carrying arguments |
| -> Signal a2 | second input signal carrying arguments |
| -> (Signal b1, Signal b2) | two output signals |
reconfig creates an synchronous adaptive process where the first signal carries
functions and the other carry the arguments. It imlements the reconfig pattern
(see reconfig22).
Constructors: reconfig[1-4][1-4].
>>>let sf = signal [(+1),(*2),(+1),(*2),(+1),(*2),(+1)]>>>let s1 = signal [1..]>>>reconfig11 sf s1{2,4,4,8,6,12,8}

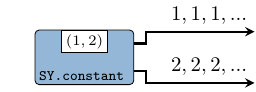
A signal generator which keeps a value constant. It implements rgw stated0X
pattern (see stated22).
Constructors: constant[1-4].
>>>let (s1, s2) = constant2 (1,2)>>>takeS 3 s1{1,1,1}>>>takeS 5 s2{2,2,2,2,2}
Arguments
| :: (b1 -> b2 -> (b1, b2)) | function to generate next value |
| -> (b1, b2) | kernel values |
| -> (Signal b1, Signal b2) | generated signals |
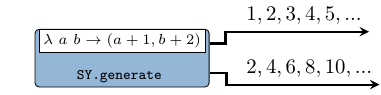
A signal generator based on a function and a kernel value. It implements the
stated0X pattern (check stated22).
Constructors: generate[1-4].
>>>let (s1,s2) = generate2 (\a b -> (a+1,b+2)) (1,2)>>>takeS 5 s1{1,2,3,4,5}>>>takeS 7 s2{2,4,6,8,10,12,14}
Arguments
| :: (b1 -> b2 -> a1 -> a2 -> (b1, b2)) | next state function |
| -> (b1, b2) | initial state values |
| -> Signal a1 | first input signal |
| -> Signal a2 | second input signal |
| -> (Signal b1, Signal b2) | output signals |
stated is a state machine without an output decoder. It implements the stated
pattern (see stated22).
Constructors: stated[1-4][1-4].
>>>let s1 = signal [1,2,3,4,5]>>>stated11 (+) 1 s1{1,2,4,7,11,16}

Arguments
| :: (b1 -> b2 -> a1 -> a2 -> (b1, b2)) | next state function |
| -> (b1, b2) | initial state values |
| -> Signal a1 | first input signal |
| -> Signal a2 | second input signal |
| -> (Signal b1, Signal b2) | output signals |
state is a state machine without an output decoder. It implements the stated
pattern (see state22).
Constructors: state[1-4][1-4].
>>>let s1 = signal [1,2,3,4,5]>>>state11 (+) 1 s1{2,4,7,11,16}

Arguments
| :: (st -> a1 -> a2 -> st) | next state function |
| -> (st -> (b1, b2)) | output decoder |
| -> st | initial state |
| -> Signal a1 | |
| -> Signal a2 | |
| -> (Signal b1, Signal b2) |
moore processes model Moore state machines. It implements the moore patterns
(see moore22).
Constructors: moore[1-4][1-4].
>>>let s1 = signal [1,2,3,4,5]>>>moore11 (+) (+1) 1 s1{2,3,5,8,12,17}

Arguments
| :: (st -> a1 -> a2 -> st) | next state function |
| -> (st -> a1 -> a2 -> (b1, b2)) | outpt decoder |
| -> st | initial state |
| -> Signal a1 | |
| -> Signal a2 | |
| -> (Signal b1, Signal b2) |
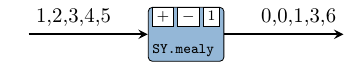
mealy processes model Mealy state machines. It implements the mealy pattern
(see mealy22).
Constructors: mealy[1-4][1-4].
>>>let s1 = signal [1,2,3,4,5]>>>mealy11 (+) (-) 1 s1{0,0,1,3,6}
Interfaces
Arguments
| :: (Num t, Ord t, Eq t) | |
| => Signal t | SY signal carrying |
| -> Signal a | first input SY signal |
| -> Signal b | second input SY signal |
| -> (SignalBase t a, SignalBase t b) | two output |
Arguments
| :: (Prod, Prod) | production rates \(p_1,p_2\) |
| -> Signal (Vector a) |
|
| -> Signal (Vector b) |
|
| -> (Signal a, Signal b) |
|
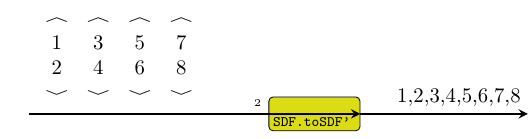
Transforms a (set of) SY signal(s) of vectors of the same length into
equivanlent SDF signal(s) by serializing the vectors according to a
production rate. If the production rate and the vector lengths do not match then a
runtime error is thrown.
Constructors: toSDF[1-4]'.
>>>let s = read "{<1,2>,<3,4>,<5,6>}" :: SY.Signal (V.Vector Int)>>>toSDF1' 2 s{1,2,3,4,5,6}
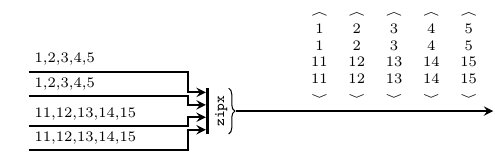
zipx :: Vector (Signal a) -> Signal (Vector a) Source #
Synchronizes all the signals contained by a vector and zips them
into one signal of vectors. It instantiates the
zipx skeleton.
>>>let s1 = SY.signal [1,2,3,4,5]>>>let s2 = SY.signal [11,12,13,14,15]>>>let v1 = V.vector [s1,s1,s2,s2]>>>v1<{1,2,3,4,5},{1,2,3,4,5},{11,12,13,14,15},{11,12,13,14,15}>>>>zipx v1{<1,1,11,11>,<2,2,12,12>,<3,3,13,13>,<4,4,14,14>,<5,5,15,15>}
unzipx :: Integer -> Signal (Vector a) -> Vector (Signal a) Source #
Unzips the vectors carried by a signal into a vector of
signals. It instantiates the unzipx
skeleton. To avoid infinite recurrence, the user needs to provide
the length of the output vector.
>>>let v1 = V.vector [1,2,3,4]>>>let s1 = SY.signal [v1,v1,v1,v1,v1]>>>s1{<1,2,3,4>,<1,2,3,4>,<1,2,3,4>,<1,2,3,4>,<1,2,3,4>}>>>unzipx 4 s1<{1,1,1,1,1},{2,2,2,2,2},{3,3,3,3,3},{4,4,4,4,4}>

unzipx' :: Signal (Vector a) -> Vector (Signal a) Source #
Same as unzipx, but "sniffs" the first event to determine the
length of the output vector. Has an unsafe behavior!
>>>let v1 = V.vector [1,2,3,4]>>>let s1 = SY.signal [v1,v1,v1,v1,v1]>>>s1{<1,2,3,4>,<1,2,3,4>,<1,2,3,4>,<1,2,3,4>,<1,2,3,4>}>>>unzipx' s1<{1,1,1,1,1},{2,2,2,2,2},{3,3,3,3,3},{4,4,4,4,4}>

