| Copyright | (c) George Ungureanu KTH/EECS/ESY 2015-2020 |
|---|---|
| License | BSD-style (see the file LICENSE) |
| Maintainer | ugeorge@kth.se |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | Safe |
| Language | Haskell2010 |
ForSyDe.Atom.MoC.SDF
Description
The SDF library implements a DSL of atoms operating according to the synchronous
dataflow model of computation, along with helpers and associated patterns.
There are many kinds of dataflow (DF) MoCs found in literature, many of which extend the original SDF formulation of [Lee87]. ForSyDe-Atom implements some of the common SDF extensions (see below), and this module exports the core atoms for all of them. As compared to other MoC sub-modules (see ForSyDe.Atom.SY.Clocked,ForSyDe.Atom.DE.React), the SDF sub-modules define only new patterns describing meaningful processes according to each DF class. The common atom semantics imply a partial order between events and operate on sequences of events, here represented with lists. As a consequence, we use the same event constructor to identify any kind of DF signal, respectively we need no MoC interface between DF domains.
Useful pointers:
- ForSyDe.Atom contains general guidelines for using the API
- the naming convention rules on how to interpret the function names based on their number of inputs and outputs.
- ForSyDe.Atom.MoC.SDF.CSDF contains patterns and utilities for cyclo-static dataflow processes.
- ForSyDe.Atom.MoC.SDF.SADF contains patterns and utilities for scenario-aware dataflow processes.
- ForSyDe.Atom.MoC.SDF.BDF contains patterns and utilities for Boolean dataflow processes.
Synopsis
- newtype SDF a = SDF {
- val :: a
- type Signal a = Stream (SDF a)
- type Prod = Int
- type Cons = Int
- signal :: [a] -> Signal a
- readSignal :: Read a => String -> Signal a
- delay :: [a] -> Signal a -> Signal a
- actor22 :: ((Cons, Cons), (Prod, Prod), [a1] -> [a2] -> ([b1], [b2])) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- delay' :: Signal a -> Signal a -> Signal a
- reconfig22 :: ((Cons, Cons), (Prod, Prod)) -> Signal ([a1] -> [a2] -> ([b1], [b2])) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- constant2 :: ([b1], [b2]) -> (Signal b1, Signal b2)
- generate2 :: ((Cons, Cons), (Prod, Prod), [b1] -> [b2] -> ([b1], [b2])) -> ([b1], [b2]) -> (Signal b1, Signal b2)
- stated22 :: ((Cons, Cons, Cons, Cons), (Prod, Prod), [b1] -> [b2] -> [a1] -> [a2] -> ([b1], [b2])) -> ([b1], [b2]) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- state22 :: ((Cons, Cons, Cons, Cons), (Prod, Prod), [b1] -> [b2] -> [a1] -> [a2] -> ([b1], [b2])) -> ([b1], [b2]) -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- moore22 :: ((Cons, Cons, Cons), Prod, [st] -> [a1] -> [a2] -> [st]) -> (Cons, (Prod, Prod), [st] -> ([b1], [b2])) -> [st] -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- mealy22 :: ((Cons, Cons, Cons), Prod, [st] -> [a1] -> [a2] -> [st]) -> ((Cons, Cons, Cons), (Prod, Prod), [st] -> [a1] -> [a2] -> ([b1], [b2])) -> [st] -> Signal a1 -> Signal a2 -> (Signal b1, Signal b2)
- toSY2 :: (Cons, Cons) -> Signal a -> Signal b -> (Signal (Vector a), Signal (Vector b))
- toSY2' :: Signal a -> Signal b -> (Signal a, Signal b)
- zipx :: Vector Cons -> Vector (Signal a) -> Signal (Vector a)
- unzipx :: Vector Prod -> Signal (Vector a) -> Vector (Signal a)
Synchronous data flow (SDF) event
The synchronous data flow (SDF) is an untimed MoC. On untimed MoCs,
[Lee98] states that: "when tags are partially ordered
rather than totally ordered, we say that the system is untimed. Untimed systems
cannot have the same notion of causality as timed systems [see
SY]. (...) Processes defined in terms of constraints on
the tags in the signals (...) have a consistent cut rather than
simultaneity." Regarding SDF, it states that "is a special case of Kahn
process networks [Kahn76]. A dataflow process is a
Kahn process that is also sequential, where the events on the self-loop signal
denote the firings of the dataflow actor. The firing rules of a dataflow actor
are partial ordering constraints between these events and events on the
inputs. (...) Produced/consumed events are defined in terms of relations with
the events in the firing signal. It results that for the same firing \(i\),
\(e_i<e_o\), as an intuitive sort of causality constraint."
A simplified definition of the ForSyDe-Atom implementation of SDF is:
- The SDF MoC
- is abstracting the execution semantics of a dataflow system where computation is performed according to firing rules where the production and the consumption rates are fixed.
Below is a depiction of the the input and the output behavior of a SDF process. Events sharing the same partial ordering in relation to a certain firing are underlined:

Implementing the SDF tag system implied a series of design decisions which lead to the following particularities:
- signals represent FIFO channels, and tags are implicit from their position in
the
Streamstructure. Internally,SDFsignals have exactly the same structure asSYsignals, whereas the partial ordering is imposed by the processes alone. - the
SDFevent constructor wraps only a value. - the order between events is partial to the firings of processes. An SDF atom will fire only when there are enough events to trigger its inputs. Once a firing occurs, it will take care of partitioning the input or output signals.
- SDF atoms require a context for executing the passed functions: the consumption \(c\) and production \(p\) rates need to be known in order to determine the behavior of a process.
- the previous statement can be synthesized into the following formal definition for the SDF execution context: \[\Gamma\vdash\alpha\rightarrow\beta = (c,p,[\alpha]_c\rightarrow[\beta]_p)\] where the indexes \(_c\) and \(_p\) suggest the mandatory lengths of the sequences of \(\alpha\) and \(\beta\) respectively. In our case, due to language limitations, \(c\) and \(p\) are passed as context arguments since they cannot be inferred from the type signature.
To see how ForSyDe-Atom implements the above definition in practice, check the
type family instance for the Fun and
Ret types.
The SDF event. It identifies a synchronous dataflow signal, and wraps only a value.
Instances
| Functor SDF Source # | Allows for mapping of functions on a SDF event. |
| Applicative SDF Source # | Allows for lifting functions on a pair of SDF events. |
| Foldable SDF Source # | |
Defined in ForSyDe.Atom.MoC.SDF.Core Methods fold :: Monoid m => SDF m -> m # foldMap :: Monoid m => (a -> m) -> SDF a -> m # foldMap' :: Monoid m => (a -> m) -> SDF a -> m # foldr :: (a -> b -> b) -> b -> SDF a -> b # foldr' :: (a -> b -> b) -> b -> SDF a -> b # foldl :: (b -> a -> b) -> b -> SDF a -> b # foldl' :: (b -> a -> b) -> b -> SDF a -> b # foldr1 :: (a -> a -> a) -> SDF a -> a # foldl1 :: (a -> a -> a) -> SDF a -> a # elem :: Eq a => a -> SDF a -> Bool # maximum :: Ord a => SDF a -> a # | |
| Traversable SDF Source # | |
| MoC SDF Source # | Implenents the SDF semantics for the MoC atoms. |
Defined in ForSyDe.Atom.MoC.SDF.Core Methods (-.-) :: Fun SDF a b -> Stream (SDF a) -> Stream (SDF b) Source # (-*-) :: Stream (SDF (Fun SDF a b)) -> Stream (SDF a) -> Stream (SDF b) Source # (-*) :: Stream (SDF (Ret SDF b)) -> Stream (SDF b) Source # (-<-) :: Stream (SDF a) -> Stream (SDF a) -> Stream (SDF a) Source # (-&-) :: Stream (SDF a) -> Stream (SDF a) -> Stream (SDF a) Source # | |
| Read a => Read (SDF a) Source # | Reads the value wrapped |
| Show a => Show (SDF a) Source # | Shows the value wrapped |
| Plottable a => Plot (Signal a) Source # | For plotting |
| type Ret SDF a Source # | |
Defined in ForSyDe.Atom.MoC.SDF.Core | |
| type Fun SDF a b Source # | |
Defined in ForSyDe.Atom.MoC.SDF.Core | |
Aliases & utilities
These are type synonyms and utilities provided for user convenience. They mainly concern the construction and usage of signals.
signal :: [a] -> Signal a Source #
Transforms a list of values into a SDF signal with only one partition, i.e. all events share the same (initial) tag.
readSignal :: Read a => String -> Signal a Source #
Reads a signal from a string. Like with the read function from
Prelude, you must specify the tipe of the signal.
>>>readSignal "{1,2,3,4,5}" :: Signal Int{1,2,3,4,5}
Process constructors
These SDF process constructors are basically specific instantiations of the patterns of atoms defined in ForSyDe.Atom.MoC.
Simple
These processes are all that is needed to create an arbitrary SDF process network.
The delay process "delays" a signal with initial events built
from a list. It is an instantiation of the delay
constructor.
>>>let s = signal [1,2,3,4,5]>>>delay [0,0,0] s{0,0,0,1,2,3,4,5}

Arguments
| :: ((Cons, Cons), (Prod, Prod), [a1] -> [a2] -> ([b1], [b2])) | function on lists of values, tupled with consumption / production rates |
| -> Signal a1 | first input signal |
| -> Signal a2 | second input signal |
| -> (Signal b1, Signal b2) | two output signals |
actor processes map combnational functions on signals and take
care of synchronization between input signals. It instantiates the
comb atom pattern (see comb22).
Constructors: actor[1-4][1-4].
>>>let s1 = signal [1..]>>>let s2 = signal [1,1,1,1,1,1,1]>>>let f [a,b,c] [d,e] = [a+d, c+e]>>>actor21 ((3,2),2,f) s1 s2{2,4,5,7,8,10}
Incorrect usage (not covered by doctest):
λ> actor21 ((3,2),3,f) s1 s2 *** Exception: [MoC.SDF] Wrong production

Composite
These are not-so-meaningful process constructors, but display interesting behavior nevertheless. While not commonly used or met in regular designs, these constructors are merely SDF instantiations of the ForSyDe.Atom.MoC patterns, showing that these patterns can be overloaded no matter the MoC they implement.
Arguments
| :: Signal a | signal containing the initial tokens |
| -> Signal a | input signal |
| -> Signal a | output signal |
Similar to the previous, but this is the raw instantiation of the
delay pattern. It appends the contents of one
signal at the head of another signal.
>>>let s1 = signal [0,0,0]>>>let s2 = signal [1,2,3,4,5]>>>delay' s1 s2{0,0,0,1,2,3,4,5}

Arguments
| :: ((Cons, Cons), (Prod, Prod)) | |
| -> Signal ([a1] -> [a2] -> ([b1], [b2])) | function on lists of values, tupled with consumption / production rates |
| -> Signal a1 | first input signal |
| -> Signal a2 | second input signal |
| -> (Signal b1, Signal b2) | two output signals |
reconfig creates an SDF adaptive process where the first signal
carries functions and the other carry the arguments. It
instantiates the reconfig atom pattern (see
reconfig22). According to our SDF definition,
the production and consumption rates need to be fixed, so they are
passed as parameters to the constructor, whereas the first signal
carries adaptive functions only. For the adaptive signal it only
makes sense that the consumption rate is always 1.
Constructors: reconfig[1-4][1-4].
>>>let f1 a = [sum a]>>>let f2 a = [maximum a]>>>let sf = signal [f1,f2,f1,f2,f1,f2,f1]>>>let s1 = signal [1..]>>>reconfig11 (4,1) sf s1{10,8,42,16,74,24,106}

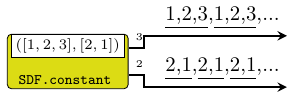
A signal generator which repeats the initial tokens
indefinitely. It is actually an instantiation of the stated0X
constructor (check stated22).
Constructors: constant[1-4].
>>>let (s1, s2) = constant2 ([1,2,3],[2,1])>>>takeS 7 s1{1,2,3,1,2,3,1}>>>takeS 5 s2{2,1,2,1,2}
Arguments
| :: ((Cons, Cons), (Prod, Prod), [b1] -> [b2] -> ([b1], [b2])) | function to generate next value, tupled with consumption / production rates |
| -> ([b1], [b2]) | values of initial tokens |
| -> (Signal b1, Signal b2) | generated signals |
A signal generator based on a function and a kernel value. It
is actually an instantiation of the stated0X constructor
(check stated22).
Constructors: generate[1-4].
>>>let f a b = ([sum a, sum a],[sum b, sum b, sum b])>>>let (s1,s2) = generate2 ((2,3),(2,3),f) ([1,1],[2,2,2])>>>takeS 7 s1{1,1,2,2,4,4,8}>>>takeS 8 s2{2,2,2,6,6,6,18,18}

Arguments
| :: ((Cons, Cons, Cons, Cons), (Prod, Prod), [b1] -> [b2] -> [a1] -> [a2] -> ([b1], [b2])) | next state function, tupled with consumption / production rates |
| -> ([b1], [b2]) | initial state partitions of values |
| -> Signal a1 | first input signal |
| -> Signal a2 | second input signal |
| -> (Signal b1, Signal b2) | output signals |
stated is a state machine without an output decoder. It is an
instantiation of the state MoC constructor (see
stated22).
Constructors: stated[1-4][1-4].
>>>let f [a] [b,c] = [a+b+c]>>>let s = signal [1,2,3,4,5,6,7]>>>stated11 ((1,2),1,f) [1] s{1,4,11,22}

Arguments
| :: ((Cons, Cons, Cons, Cons), (Prod, Prod), [b1] -> [b2] -> [a1] -> [a2] -> ([b1], [b2])) | next state function, tupled with consumption / production rates |
| -> ([b1], [b2]) | initial partitions of values |
| -> Signal a1 | first input signal |
| -> Signal a2 | second input signal |
| -> (Signal b1, Signal b2) | output signals |
state is a state machine without an output decoder. It is an
instantiation of the stated MoC constructor (see
state22).
Constructors: state[1-4][1-4].
>>>let f [a] [b,c] = [a+b+c]>>>let s = signal [1,2,3,4,5,6,7]>>>state11 ((1,2),1,f) [1] s{4,11,22}

Arguments
| :: ((Cons, Cons, Cons), Prod, [st] -> [a1] -> [a2] -> [st]) | next state function, tupled with consumption / production rates |
| -> (Cons, (Prod, Prod), [st] -> ([b1], [b2])) | output decoder, tupled with consumption / production rates |
| -> [st] | initial state values |
| -> Signal a1 | |
| -> Signal a2 | |
| -> (Signal b1, Signal b2) |
moore processes model Moore state machines. It is an
instantiation of the moore MoC constructor (see
moore22).
Constructors: moore[1-4][1-4].
>>>let ns [a] [b,c] = [a+b+c]>>>let od [a] = [a+1,a*2]>>>let s = signal [1,2,3,4,5,6,7]>>>moore11 ((1,2),1,ns) (1,2,od) [1] s{2,2,5,8,12,22,23,44}

Arguments
| :: ((Cons, Cons, Cons), Prod, [st] -> [a1] -> [a2] -> [st]) | next state function, tupled with consumption / production rates |
| -> ((Cons, Cons, Cons), (Prod, Prod), [st] -> [a1] -> [a2] -> ([b1], [b2])) | outpt decoder, tupled with consumption / production rates |
| -> [st] | initial state values |
| -> Signal a1 | |
| -> Signal a2 | |
| -> (Signal b1, Signal b2) |
mealy processes model Mealy state machines. It is an
instantiation of the mealy MoC constructor
(see mealy22).
Constructors: mealy[1-4][1-4].
>>>let ns [a] [b,c] = [a+b+c]>>>let od [a] [b] = [a+b,a*b]>>>let s = signal [1,2,3,4,5,6,7]>>>mealy11 ((1,2),1,ns) ((1,1),2,od) [1] s{2,1,6,8,14,33,26,88}
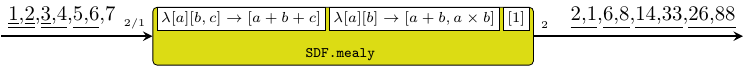
Interfaces
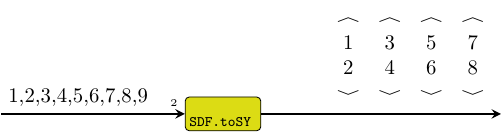
Arguments
| :: (Cons, Cons) | consumption rate of interface process |
| -> Signal a |
|
| -> Signal b |
|
| -> (Signal (Vector a), Signal (Vector b)) |
|
Transforms a (set of) SDF signal(s) into the equivalent
SY signal(s). The partial ordering is transformed to total
ordering with respect to the firings of the interface process(es), and events
consumed during one firing are grouped into vectors.
Constructors: toSY[1-4].
>>>let s = SDF.signal [1,2,3,4,5,6,7,8,9]>>>toSY1 2 s{<1,2>,<3,4>,<5,6>,<7,8>}
Alternative implementation to toSY2, where the consumption rate of the
interface process is 1, meaning that each SDF event has a corresponding SY event.
Constructors: toSY[1-4]'.
>>>let s = SDF.signal [1,2,3,4,5]>>>toSY1' s{1,2,3,4,5}

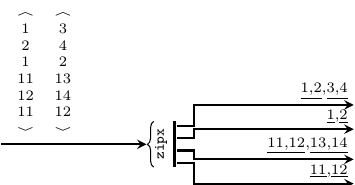
Arguments
| :: Vector Cons | consumption rates |
| -> Vector (Signal a) | vector of signals |
| -> Signal (Vector a) | signal of vectors |
Consumes tokens from a vector of signals and merges them into a
signal of vectors, with a production rate of 1. It instantiates the
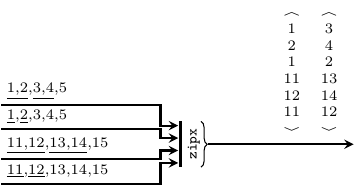
zipx skeleton.
>>>let s1 = SDF.signal [1,2,3,4,5]>>>let s2 = SDF.signal [11,12,13,14,15]>>>let v1 = V.vector [s1,s1,s2,s2]>>>let r = V.vector [2,1,2,1]>>>v1<{1,2,3,4,5},{1,2,3,4,5},{11,12,13,14,15},{11,12,13,14,15}>>>>zipx r v1{<1,2,1,11,12,11>,<3,4,2,13,14,12>}
Arguments
| :: Vector Prod | production rates (in reverse order) |
| -> Signal (Vector a) | signal of vectors |
| -> Vector (Signal a) | vector of signals |
Consumes the vectors carried by a signal with a rate of 1, and
unzips them into a vector of signals based on the user provided
rates. It instantiates the unzipx
skeleton.
OBS: due to the recur pattern
contained by unzipx, the vector of
production rates needs to be provided in reverse order (see
ForSyDe.Atom.Skel.Vector).
>>>let s1 = SDF.signal [1,2,3,4,5]>>>let s2 = SDF.signal [11,12,13,14,15]>>>let v1 = V.vector [s1,s1,s2,s2]>>>let r = V.vector [2,1,2,1]>>>let sz = zipx r v1>>>v1<{1,2,3,4,5},{1,2,3,4,5},{11,12,13,14,15},{11,12,13,14,15}>>>>sz{<1,2,1,11,12,11>,<3,4,2,13,14,12>}>>>unzipx (V.reverse r) sz<{1,2,3,4},{1,2},{11,12,13,14},{11,12}>