| Copyright | (c) George Ungureanu KTH/EECS/ESY 2019-2020 |
|---|---|
| License | BSD-style (see the file LICENSE) |
| Maintainer | ugeorge@kth.se |
| Stability | experimental |
| Portability | portable |
| Safe Haskell | Safe |
| Language | Haskell2010 |
ForSyDe.Atom.Skel.Vector.DSP
Description
This module exports a set of Vector patterns commonly used in signal processing
designs.
Synopsis
- taylor :: (Eq a, Floating a) => Int -> Int -> a -> Vector a
- taylor' :: (Eq a, Floating a) => p -> a -> Vector a
- dotvv :: Num a => Vector a -> Vector a -> a
- dotvm :: Num a => Vector a -> Vector (Vector a) -> Vector a
- dotvv' :: Num a => ((a -> a -> a) -> f a -> f a -> f a) -> Vector (f a) -> Vector (f a) -> f a
- dotvm' :: (b -> b -> b) -> (a -> b -> b) -> Vector a -> Vector (Vector b) -> Vector b
- dotmv' :: (a -> a -> a) -> (b -> a -> a) -> Vector (Vector b) -> Vector a -> Vector a
- hanning :: Floating n => Int -> Vector n
- hamming :: Floating n => Int -> Vector n
- blackman :: Floating n => Int -> Vector n
- fir :: Num a => Vector a -> Vector a -> Vector a
- fir' :: (a -> a -> a) -> (c -> a -> a) -> (a -> a) -> Vector c -> a -> a
- twiddles :: Floating a => Int -> Vector (Complex a)
- fft :: RealFloat a => Int -> Vector (Complex a) -> Vector (Complex a)
- fft' :: Floating a => (Complex a -> a -> a -> (a, a)) -> Int -> Vector a -> Vector a
- duals :: Vector a -> (Vector a, Vector a)
- unduals :: Vector a -> Vector a -> Vector a
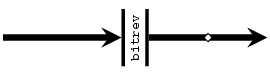
- bitrev :: Vector a -> Vector a
Documentation
Arguments
| :: (Eq a, Floating a) | |
| => Int | number of points in the output window. |
| -> Int | Number of nearly constant level sidelobes adjacent to the mainlobe |
| -> a | Desired peak sidelobe level in decibels (db) relative to the mainlobe |
| -> Vector a | The window, with the center value normalized to one (the value one appears only if the number of samples is odd). |
Return the Taylor window. The Taylor window allows for a selectable sidelobe suppression with a minimum broadening. This window is commonly used in radar processing [1]. Code inspired from a pull request for SciPy.
Reference:
[1] W. Carrara, R. Goodman, and R. Majewski "Spotlight Synthetic Aperture Radar: Signal Processing Algorithms" Pages 512-513, July 1995.
taylor' :: (Eq a, Floating a) => p -> a -> Vector a Source #
Returns a Taylor window with default arguments: 4 sidelobes, and peak sidelobe level of -30dB
dotvm :: Num a => Vector a -> Vector (Vector a) -> Vector a Source #
Calculates the dot product between a vector and a matrix
Arguments
| :: (b -> b -> b) | kernel function for a row/column reduction, e.g. |
| -> (a -> b -> b) | binary operation for pair-wise elements, e.g. |
| -> Vector a | length = |
| -> Vector (Vector b) | size = |
| -> Vector b | length = |
Higher order version of dotvm. Implements the template for a dot operation
between a vector and a matrix.
>>>let mA = vector [vector[1,-1,1], vector[1,-1,-1], vector[1,1,-1], vector[1,1,1]]>>>let y = vector[1,0,0,0]>>>dotVecMat (+) (*) mA y<1,1,1,1>
Arguments
| :: (a -> a -> a) | kernel function for a row/column reduction, e.g. |
| -> (b -> a -> a) | binary operation for pair-wise elements, e.g. |
| -> Vector (Vector b) | size = |
| -> Vector a | length = |
| -> Vector a | length = |
Higher order pattern implementing the template for a dot operation between a vector and a matrix.
>>>let mA = vector [vector[1,-1,1], vector[1,-1,-1], vector[1,1,-1], vector[1,1,1]]>>>let y = vector[1,0,0,0]>>>dotVecMat (+) (*) mA y<1,1,1,1>
Compute a Hanning window.
Inspired from https://hackage.haskell.org/package/sdr-0.1.0.6/src/hs_sources/SDR/FilterDesign.hs
Compute a Hamming window.
Inspired from https://hackage.haskell.org/package/sdr-0.1.0.6/src/hs_sources/SDR/FilterDesign.hs
Compute a Blackman window.
Inspired from https://hackage.haskell.org/package/sdr-0.1.0.6/src/hs_sources/SDR/FilterDesign.hs
Arguments
| :: Num a | |
| => Vector a | vector of coefficients |
| -> Vector a | input vector of numbers; size = |
| -> Vector a | output vector of numbers; size = |
Moving average filter (FIR) on numbers, applied in reverse order (more optimized).
>>>let v = vector [0,0,0,0,0,1]>>>let c = vector [1,2,3]>>>fir c<0,0,0,3,2,1>
Arguments
| :: (a -> a -> a) | process/operation replacing |
| -> (c -> a -> a) | process/operation replacing |
| -> (a -> a) | delay process |
| -> Vector c | vector of coefficients |
| -> a | input signal/structure |
| -> a | output signal/structure |
Higher order version of fir. Can create a systolic FIR process network. See
[Ungureanu20a] for a discussion on the relation
between fir and fir'.
>>>let c = vector [1,2,3]>>>let s = SY.signal [1,0,0,0,0,0,0,0]>>>fir' (SY.comb21 (+)) (\c -> SY.comb11 (*c)) (SY.delay 0) c s{3,2,1,0,0,0,0,0}
twiddles :: Floating a => Int -> Vector (Complex a) Source #
generates the "twiddle" coefficients for a FFT network.
Arguments
| :: RealFloat a | |
| => Int | number of FFT stages ( |
| -> Vector (Complex a) | |
| -> Vector (Complex a) |
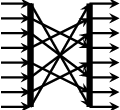
Radix-2 decimation-in-frequecy Fast Fourier Transform, applied on numbers. For the difference between DIT- and DIF-FFT, see https://www.slideshare.net/chappidi_saritha/decimation-in-time-and-frequency
Arguments
| :: Floating a | |
| => (Complex a -> a -> a -> (a, a)) | "butterfly" function. |
| -> Int | number of FFT stages ( |
| -> Vector a | |
| -> Vector a |
Higher order version of fft. Takes the "butterfly" function as argument.
butterfly w x0 x1 = let t = w * x1 in (x0 + t, x0 - t) fft' butterfly === fft
duals :: Vector a -> (Vector a, Vector a) Source #
splits a vector in two equal parts.
>>>duals $ vector [1,2,3,4,5,6,7](<1,2,3>,<4,5,6>)